Axiomatic set theory is a formal system that defines and studies sets using a collection of axioms, or basic rules. Unlike the naive set theory, which allows the definition of any set, axiomatic set theory imposes restrictions to avoid contradictions like Russell’s Paradox (the paradox of the set of all sets that do not contain themselves).1. Introduction
Set theory, the study of collections of objects or “sets,” serves as a foundational framework for modern mathematics. Sets, at their core, allow mathematicians to define and manipulate collections of numbers, shapes, or even other sets, making it crucial for fields like algebra, topology, and logic. However, the intuitive nature of set theory can give rise to contradictions, such as Russell’s paradox, which questions the existence of sets that contain themselves.
To resolve these issues and provide a rigorous foundation, a formal system was necessary. Axiomatic set theory emerged as this formal framework, where clear rules and axioms are defined to avoid inconsistencies. It establishes the basic principles governing how sets behave, ensuring logical coherence across mathematics.
Historical Background
Set theory was pioneered in the late 19th century by Georg Cantor, who introduced the concept of infinity in mathematical terms through his study of infinite sets. His work laid the groundwork for much of modern mathematics, but it also uncovered certain paradoxes that challenged the internal consistency of set theory. Russell’s paradox, for example, revealed a fundamental issue with naive set theory: Can a set contain itself as a member?
In response to these challenges, mathematicians sought a more formal structure for set theory. Ernst Zermelo, in 1908, introduced a system of axioms that aimed to eliminate such paradoxes by restricting how sets can be defined. His work was further refined by Abraham Fraenkel, leading to the development of the Zermelo-Fraenkel set theory (ZF). When paired with the Axiom of Choice, this system is known as Zermelo-Fraenkel set theory with Choice (ZFC), which remains the most widely accepted foundation for mathematics today.
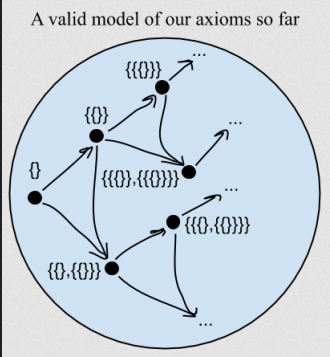
Zermelo-Fraenkel Set Theory (ZFC)
Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC) is the most widely accepted version of axiomatic set theory, serving as the foundational framework for much of modern mathematics. ZFC defines a formal system of rules that governs the behavior of sets, eliminating paradoxes that plagued earlier set theories, such as Russell’s paradox. By relying on a precise set of axioms, ZFC ensures the internal consistency of mathematics, enabling mathematicians to define sets and reason about them in a rigorous way.
ZFC plays a crucial role in mathematics by providing a unified framework for almost every mathematical discipline, from algebra to topology. It allows for the study of both finite and infinite sets, which are fundamental in fields like calculus, analysis, and number theory. Through its carefully formulated axioms, ZFC provides a robust foundation that prevents logical contradictions while remaining flexible enough to support the entire structure of mathematical theory.
Key Axioms in ZFC
- Axiom of Extensionality: This axiom states that a set is completely determined by its elements. In other words, two sets are considered equal if and only if they have the same members. This ensures that the identity of a set is defined by what it contains, not by any other characteristic.
- Axiom of Pairing: This axiom allows for the creation of a new set containing exactly two elements. Given any two sets, the axiom guarantees that there exists another set, called a pair, which contains exactly these two sets. This is fundamental for constructing ordered pairs and forming more complex structures like Cartesian products.
- Axiom of Union: This axiom allows for the creation of larger sets from existing sets. Specifically, given a set of sets, the union of those sets forms a new set containing all the elements of each individual set. This is important for operations like merging sets or constructing infinite collections.
- Axiom of Power Set: According to this axiom, for any given set, there exists another set that contains all possible subsets of the original set. This “power set” is essential for studying relationships between sets, including functions, relations, and cardinality.
- Axiom of Infinity: This axiom guarantees the existence of an infinite set, typically taken as the set of natural numbers. This axiom is crucial for the development of number theory, analysis, and many areas of mathematics that rely on the concept of infinity, including calculus and the study of infinite sequences and series.
The Axiom of Choice
The Axiom of Choice (AC) is one of the most debated axioms in Zermelo-Fraenkel set theory, known for its powerful yet controversial implications. It states that given any collection of non-empty sets, it is possible to choose exactly one element from each set, even if there is no explicit rule for making the choices. While this might seem intuitive, its non-constructive nature — meaning it allows for the existence of sets without explicitly defining them — has led to significant philosophical and mathematical debates.
One of the most striking consequences of the Axiom of Choice is the Banach-Tarski paradox, which asserts that it is possible to decompose a solid ball into a finite number of pieces and then reassemble those pieces into two identical copies of the original ball. This paradox defies geometric intuition but is mathematically valid, demonstrating the far-reaching implications of the Axiom of Choice.
The Axiom of Choice plays a crucial role in many mathematical proofs and constructions, particularly in areas such as topology and functional analysis. It enables the existence of certain objects that cannot be explicitly constructed, such as bases for infinite-dimensional vector spaces. Despite its controversy, the Axiom of Choice is widely accepted because of its essential role in simplifying complex mathematical proofs and enabling the existence of otherwise unattainable results.
Applications and Impact of Axiomatic Set Theory
Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC) underpins a wide range of mathematical fields, providing a unified framework for various branches of mathematics. In algebra, ZFC is essential for defining structures like groups, rings, and fields, ensuring that these mathematical objects are rigorously defined and free from contradictions. Topology also relies on set theory, particularly in the study of open sets, compactness, and the continuum, where the Axiom of Choice often plays a crucial role in establishing results like Tychonoff’s theorem.
In logic, ZFC serves as the foundational framework for formal systems and proofs, ensuring consistency in reasoning about mathematical objects. The theory also provides the basis for defining infinite sets and functions, which are crucial in areas like analysis and calculus. For example, set theory is fundamental to the concept of cardinality, which compares the sizes of infinite sets, distinguishing between countable and uncountable infinities.
Overall, axiomatic set theory is vital in constructing mathematical structures and ensuring the internal coherence of mathematical theories. It forms the backbone of much of modern mathematics, providing tools and frameworks that are indispensable for theoretical developments.
Conclusion
Axiomatic set theory, particularly in the form of ZFC, plays a pivotal role in ensuring the consistency and logical coherence of modern mathematics. By formalizing the concept of sets and eliminating paradoxes like Russell’s paradox, ZFC provides a solid foundation for a wide range of mathematical fields. The Axiom of Choice, while controversial, is an essential component that allows for the construction of sets and the proof of important theorems across disciplines.
The impact of axiomatic set theory is vast, enabling mathematicians to work with infinite sets, define complex mathematical structures, and explore abstract concepts in a rigorous manner. In doing so, it continues to serve as a cornerstone of mathematical reasoning and exploration.
References/Further Reading
- Thomas Jech, Set Theory, Springer-Verlag, 3rd edition, 2003.
(Comprehensive introduction to Zermelo-Fraenkel set theory and the Axiom of Choice.) - Paul Halmos, Naive Set Theory, Springer, 1960.
(Classic introductory text on set theory and its foundational role in mathematics.) - Wolfram MathWorld, Zermelo-Fraenkel Set Theory (ZFC).
Wolfram MathWorld – ZFC - Stanford Encyclopedia of Philosophy, Set Theory.
Stanford Encyclopedia of Philosophy – Set Theory - SpringerLink, Banach-Tarski Paradox.
SpringerLink – Banach-Tarski Paradox
FAQ :
- What is Zermelo-Fraenkel set theory (ZFC)?
ZFC is the most widely accepted form of axiomatic set theory, providing a formal framework to study sets and avoid paradoxes like Russell’s paradox. - Why is the Axiom of Choice controversial?
The Axiom of Choice is non-constructive, allowing for the existence of sets without explicitly defining them. This leads to counterintuitive results like the Banach-Tarski paradox. - What is the Banach-Tarski paradox?
It’s a result that, under the Axiom of Choice, a solid ball can be split into pieces and reassembled into two identical balls, defying physical intuition. - Why is axiomatic set theory important in mathematics?
Axiomatic set theory provides a rigorous foundation for various mathematical fields, ensuring consistency and allowing for the study of infinite sets and complex structures. - What are some key axioms in ZFC?
Important axioms include the Axiom of Extensionality (sets defined by elements), Pairing, Union, Power Set, and Infinity, each governing how sets can be constructed and interact. - How does ZFC apply to different branches of mathematics?
ZFC underpins fields like algebra, topology, and logic by providing the tools to define mathematical objects and reason about their properties systematically. - How does the Axiom of Infinity relate to mathematics?
It ensures the existence of infinite sets, which is essential for the development of number theory, analysis, and concepts like sequences and limits.
